Phibonacci, or actually, Fibonacci, was a man once known as Leonardo of Pisa in Italy around the 13th century A.D.

Today we know this name, and the associated Greek letter ø or “Phi”, in relation to the spiraling sequence of numbers that form a ‘golden spiral’. I recently learned there are silver and bronze spirals as well, but this article will only be focusing on the Golden Ratio, Phi, and the Fibonacci sequence.

Phi has a few interesting properties, one of them being what happens when you ‘square’ it, which simply means multiplying it by itself; which when happens, equals one plus itself, or 2.618…

But what about the cube of Phi, (Phi x Phi x Phi)? Or how about Phi to the fourth power, and so forth…

As it turns out, the Fibonacci sequence is hidden in these mathematical expressions, it’s just not that obvious, so I’m not sure if anyone has pointed this out before.

It is even more evident when you take the squares and invert them.  (One divided by Phi squared, One divided by Phi cubed, etc)

Note that One divided by Phi is the same thing as Phi to the power of negative one.

This following chart should easily illustrate what I’m trying to say.  Phi is 1.618..etc  and Phi to the power of negative one, two, etc. is shown below.  A lot more could be said here but I’ll let this picture speak for itself.  It appears Leonardo’s sequence is embedded into the powers of the golden number, which kinda does make sense.

The -1 means Phi to the power of negative one, etc.

I’ve made illustrations similar to this one before, but didn’t realize the Fibonacci sequence could be found further and further down in the powers of Phi. 

NERD WARNING: THE FOLLOWING IS SUPER TECHNICAL AND NERDY – YOU HAVE BEEN WARNED!

PhiBonacci by Joe Dubs

The Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Phi with 144 digits:

1.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748475408807538689175212663386222353693179318 <– 144 digits not counting the 1 (the next digits are 00)

Negative Powers of Phi with 50 digits after decimal: (last digit may be rounded up)

Phi = 1.61803398874989484820458683436563811772030917980576

-1 = 0.61803398874989484820458683436563811772030917980576

-2 = 0.38196601125010515179541316563436188227969082019424

-3 = 0.23606797749978969640917366873127623544061835961153

-4 = 0.14589803375031545538623949690308564683907246058271

-5 = 0.09016994374947424102293417182819058860154589902881

-6 = 0.05572809000084121436330532507489505823752656155390

-7 = 0.03444185374863302665962884675329553036401933747492

-8 = 0.02128623625220818770367647832159952787350722407898

-9 = 0.01315561749642483895595236843169600249051211339594

-10 = 0.00813061875578334874772410988990352538299511068304

-11 = 0.00502499874064149020822825854179247710751700271289

-12 = 0.00310562001514185853949585134811104827547810797015

-13 = 0.00191937872549963166873240719368142883203889474275

-14 = 0.00118624128964222687076344415442961944343921322740

-15 = 0.00073313743585740479796896303925180938859968151535

-16 = 0.00045310385378482207279448111517781005483953171206

-17 = 0.00028003358207258272517448192407399933376014980329

-18 = 0.00017307027171223934761999919110381072107938190876

-19 = 0.00010696331036034337755448273297018861268076789453

-20 = 0.00006610696135189597006551645813362210839861401424

-21 = 0.00004085634900844740748896627483656650428215388029

-22 = 0.00002525061234344856257655018329705560411646013395

-23 = 0.00001560573666499884491241609153951090016569374634

-24 = 0.00000964487567844971766413409175754470395076638761

-25 = 0.00000596086098654912724828199978196619621492735873

-26 = 0.00000368401469190059041585209197557850773583902888

-27 = 0.00000227684629464853683242990780638768847908832985

-28 = 0.00000140716839725205358342218416919081925675069902

-29 = 0.00000086967789739648324900772363719686922233763083

-30 = 0.00000053749049985557033441446053199395003441306819

-31 = 0.00000033218739754091291459326310520291918792456264

-32 = 0.00000020530310231465741982119742679103084648850554

-33 = 0.00000012688429522625549477206567841188834143605710

-34 = 0.00000007841880708840192504913174837914250505244844

-35 = 0.00000004846548813785356972293393003274583638360865

-36 = 0.00000002995331895054835532619781834639666866883979

-37 = 0.00000001851216918730521439673611168634916771476886

-38 = 0.00000001144114976324314092946170666004750095407093

-39 = 0.00000000707101942406207346727440502630166676069794

-40 = 0.00000000437013033918106746218730163374583419337299

-41 = 0.00000000270088908488100600508710339255583256732495

-42 = 0.00000000166924125430006145710019824119000162604804

-43 = 0.00000000103164783058094454798690515136583094127691

-44 = 0.00000000063759342371911690911329308982417068477112

-45 = 0.00000000039405440686182763887361206154166025650579

-46 = 0.00000000024353901685728927023968102828251042826533

-47 = 0.00000000015051539000453836863393103325914982824047

-48 = 0.00000000009302362685275090160574999502336060002486

-49 = 0.00000000005749176315178746702818103823578922821560

-50 = 0.00000000003553186370096343457756895678757137180926

-51 = 0.00000000002195989945082403245061208144821785640635

-52 = 0.00000000001357196425013940212695687533935351540291

-53 = 0.00000000000838793520068463032365520610886434100344

-54 = 0.00000000000518402904945477180330166923048917439948

-55 = 0.00000000000320390615122985852035353687837516660396

-56 = 0.00000000000198012289822491328294813235211400779552

-57 = 0.00000000000122378325300494523740540452626115880844

-58 = 0.00000000000075633964521996804554272782585284898707

-59 = 0.00000000000046744360778497719186267670040830982137

-60 = 0.00000000000028889603743499085368005112544453916570

Positive Powers of Phi with 50 digits after decimal: (last digit may be rounded up)

1 = 1.61803398874989484820458683436563811772030917980576

2 = 2.61803398874989484820458683436563811772030917980576

3 = 4.23606797749978969640917366873127623544061835961153

4 = 6.85410196624968454461376050309691435316092753941729

5 = 11.09016994374947424102293417182819058860154589902881

6 = 17.94427190999915878563669467492510494176247343844610

7 = 29.03444185374863302665962884675329553036401933747492

8 = 46.97871376374779181229632352167840047212649277592102

9 = 76.01315561749642483895595236843169600249051211339594

10 = 122.99186938124421665125227589011009647461700488931696

11 = 199.00502499874064149020822825854179247710751700271289

12 = 321.99689437998485814146050414865188895172452189202985

13 = 521.00191937872549963166873240719368142883203889474275

14 = 842.99881375871035777312923655584557038055656078677260

15 = 1364.00073313743585740479796896303925180938859968151535

16 = 2206.99954689614621517792720551888482218994516046828794

17 = 3571.00028003358207258272517448192407399933376014980329

18 = 5777.99982692972828776065238000080889618927892061809124

19 = 9349.00010696331036034337755448273297018861268076789453

20 = 15126.99993389303864810402993448354186637789160138598576

21 = 24476.00004085634900844740748896627483656650428215388029

22 = 39602.99997474938765655143742344981670294439588353986605

23 = 64079.00001560573666499884491241609153951090016569374634

24 = 103681.99999035512432155028233586590824245529604923361239

25 = 167761.00000596086098654912724828199978196619621492735873

26 = 271442.99999631598530809940958414790802442149226416097112

27 = 439204.00000227684629464853683242990780638768847908832985

28 = 710646.99999859283160274794641657781583080918074324930098

29 = 1149851.00000086967789739648324900772363719686922233763083

30 = 1860497.99999946250950014442966558553946800604996558693181

It doesn’t appear there is too much going on with the positive powers of Phi, but you just have to look a little closer….

To understand what is going on here:

Phi ^ 30 is about 1860497.9999994625095…

and

Phi ^ -30 is about 0.0000005374904…

Adding these inverse values together is always going to approach nearly a whole number.

In this case it is 1860497.9999999999999…

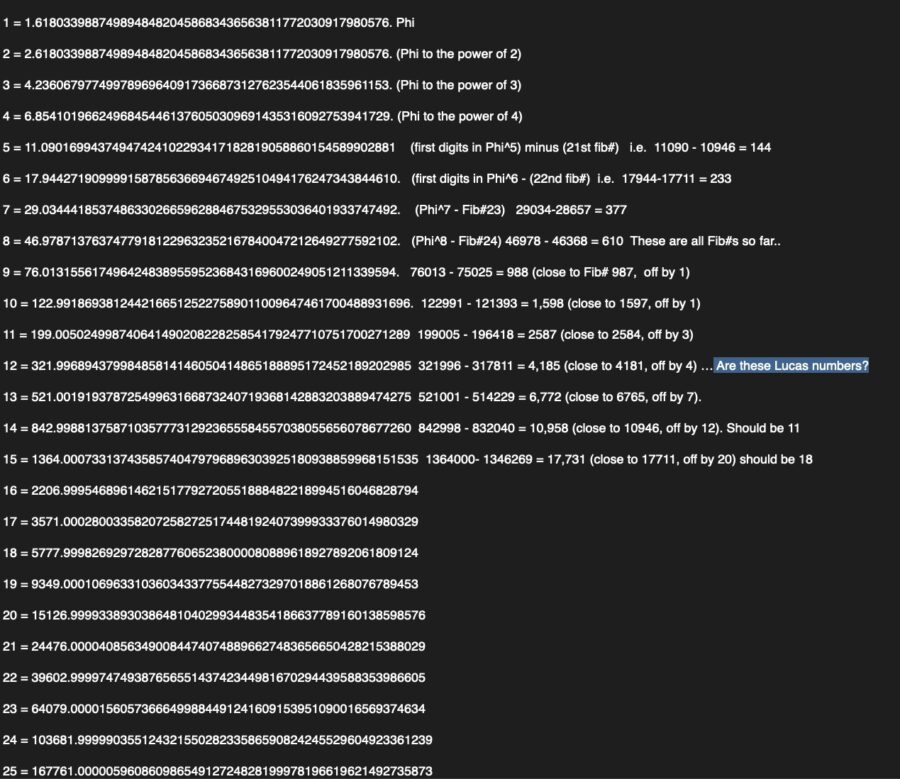
The powers of positive Phi also show the Fibonacci sequence, but only if you subtract them from a number above the value, and only when you look at every other number:

For example Phi^ 6 = 17.9442719

But when you subtract it from 17.99999999 it equals 0.05572809

1.9999999 – Phi ^1 = 0.38196601 (same value as next value, which is weird)

2.9999999 – Phi ^2 = 0.38196601 (not very close to 377)

4.9999999 – Phi ^3 = 0.76393202   (where Phi ^ 3 = 4.236067977 (not very close to 233)

6.9999999 – Phi ^4 = 0.14589802 (note this is close to 144)

11.9999999 – Phi ^5 = 0.90983005 (where Phi ^ 5 = 11.09016994 (note this is NEARLY 089)

17.9999999 – Phi ^6 = 0.05572809

29.9999999 – Phi ^7 = 0.96555813    (where Phi ^7 = 29.03444185

46.9999999 – Phi ^8 = 0.02128622

76.9999999 – Phi ^9 = 0.98684437    (where Phi ^9 = 76.01315561

122.9999999 – Phi^10 = 0.00813060

199.9999999 – Phi^11 = 0.99497499    (where Phi ^11 = 199.0050249

321.9999999 – Phi^12 = 0.00310561

521.9999999 – Phi^13 = 0.99808061 (where Phi ^13 = 521.0019193 (note this is NEARLY 002)

46.9999999 – Phi^14 = 0.00118623

1364.9999999 – Phi^15 = 0.99926685 (where Phi ^15 = 1364.0007331(note this is close to 001)

2206.9999999 – Phi ^16 = 0.00045310

Keep in mind the Fibonacci Sequence is:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, etc

^The immediate numbers above might be hard to read depending on what device you are reading on, so here is a picture that better visualizes what I’m trying to say…

The pattern builds itself up only to break down again further up the powers of Phi.

So, without rounding, we have seven Fibonacci numbers in a row if we recognize the rule above about varying every other number and taking the whole number above the positive power of Phi and subtracting it to find the Fibonacci number pattern. Wow that is a mouthful. 

The negative powers of Phi (shown above) also have the same seven numbers.(shown in green towards the top of this article) 

It seems there is something special about these seven numbers, and perhaps the number seven itself.

[3, 5, 8, 13, 21, 34, and 55]

These numbers show up in both the negative and positive powers of Phi, the Golden Number.

Just for fun, if we add these numbers up it totals 139, which is the 34th prime number, and 34 is the tenth number of our favorite sequence.

Thanks for reading. I know that was super nerdy. My next article will about something entirely different, promise.

*Update. May 11th 2023

It looks like the Lucas Number pattern is partially hidden in there too! (1,3,4,7..)

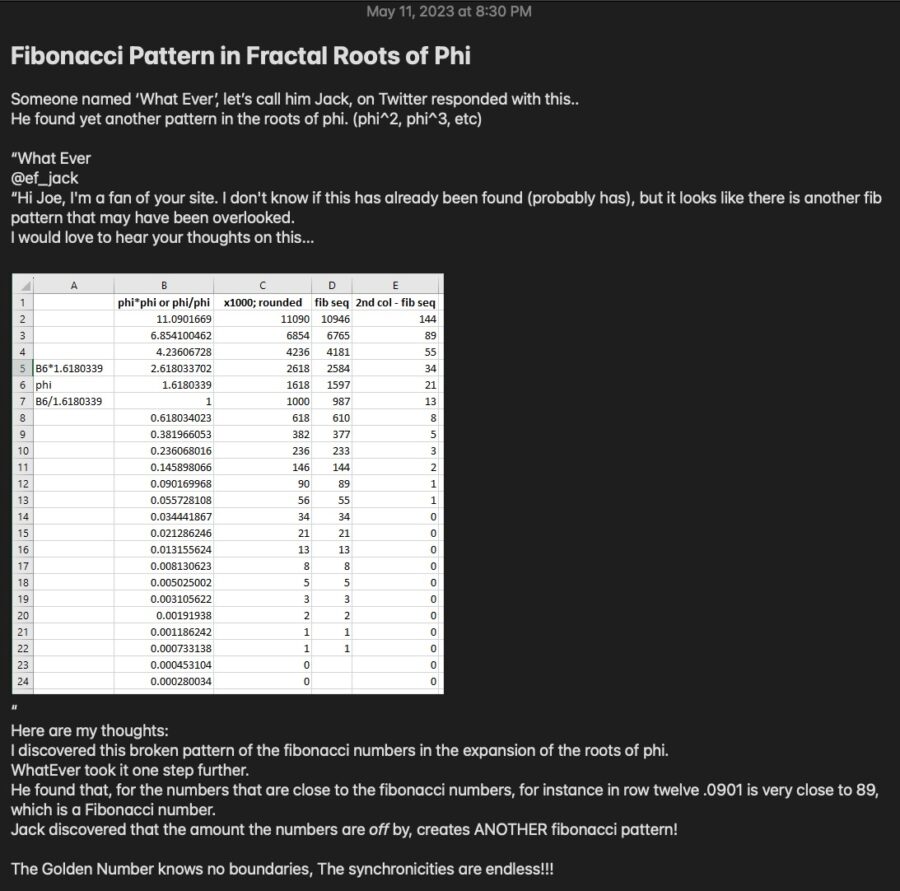
Hi Joe, I'm a fan of your site. I don't know if this has already been found (probably has), but it looks like there is another fib pattern that may have been overlooked.
I would love to hear your thoughts on this…https://t.co/Zrm3gnXU3T

— What Ever (@ef_jack) May 11, 2023

Thanks for attending my Tech Ted Talk!