The Archimedean Solids & Their Dual Catalan Solids

The Archimedean solids and their duals the Catalan solids are less well known than the Platonic solids.  Whereas the Platonic solids are composed of one shape, these forms that Archimedes wrote about are made of at least two different shapes, all forming identical vertices.  They are 13 polyhedra of this type.  And since each solid has a ‘dual’ there are also 13 Catalan solids.  There are 26 in total.  If  our two-dimensional letters of the alpha-bet were three dimensional forms, these solids would be a great representation of our language.

The Archimedean Solids

Five Archimedean solids (on the bottom of illustration above) are derived from the Platonic solids by truncating or ‘cutting off’ the corners of each form.

The Platonic Solids

The vertices of the dual of a solid are the midpoints of the faces of the original solid.  Among the Platonic solids, the octahedron and cube are duals of each other.  The dodecahedron is the dual of the icosahedron.  The last of these five solids is the tetrahedron which is a dual of itself when turned 180 degrees.

The Catalan Solids are the duals of the Archimedean solids.  Named after belgian mathematician Eugène Catalan in 1865, these are made by placing a point in the middle of the faces of the Archimedean Solids and joining the points together with straight lines.

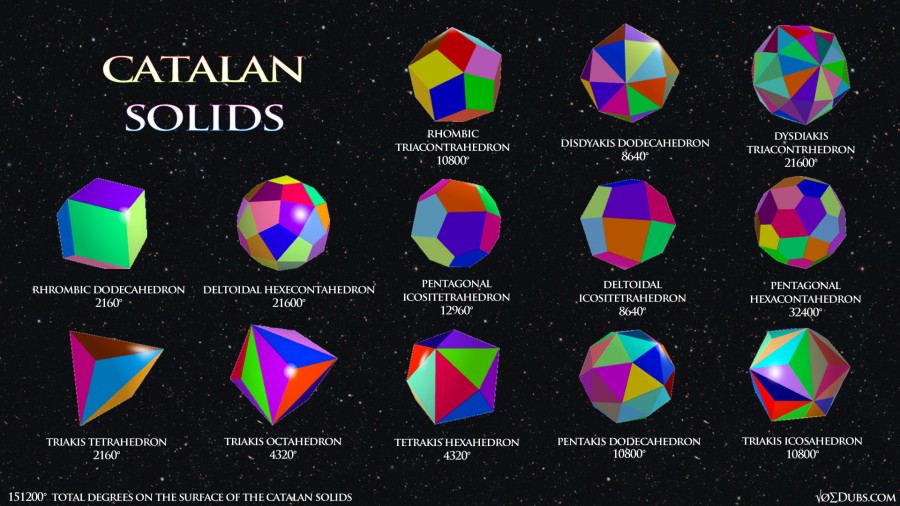
The Catalan Solids

The Archimedean and dual Catalan Solids

The number below each solid shows the sum of the angles on its surface.  Since the cuboctahedron (in blue and purple on the left) is composed of 8 triangles and 6 squares, its surface contains a total of 3600°.  Each triangle is made of 180° and each square 360°.  (180° x 8) + (360° x 6) = 3600°

If found it interesting that 4 of the 13 Archimedean solids have surfaces that sum 7920°.  7920 is a number that seems to pop up frequently, not only as the mean diameter of earth in miles (credit: Not A Scientist Around), but also the total number of protons & neutrons used by the 64 Codons that make up our DNA (credit: Anthony Morris).  7920 is also encoded into our units of measure, since 7920 inches = 1 furlong, and 7920 feet is exactly a mile and a half.  792 is also found in the bible as the diameter of New Jerusalem, being exactly 7,920,000 ft. (credit Randall Carlson).

The octahedron is to the Platonic solids; as the truncated cuboctahedron is to the Archimedean solids.  The total angular measure of the Platonic solids equals 14,400° with the octahedron being exactly 1/10th of this number (1440°).  The same is true for the truncated cuboctahedron (16560°), when compared to the total amount of degrees in the Archimedean solids (165600°).

Base-10, and the recurrence of ‘ten’ are evident in the Platonic solids.  There are exactly 5 x 10 sides among them, and 9 x 10 edges.  If we contrive this base 10 symbolism a bit we can find 200, as the total number of sides, edges, points, and shapes used to make these 3-dimensional forms.

Ten is more than a number, it’s a concept for organizing reality.  In other words, ten is not ‘ten’ because man decided that’s when we are going to stop using the single digit (9), or single glyph, or single shape, and add this concept of nothing (zero) behind it in order to create fractal scalability and retractability.

The Archimedean solids are further evidence of the way nature operates by using these canonical numerical archetypes to conceptually create what we know as reality, numerically, geometrically, musically, and cosmically.

“A man should hear a little music, read a little poetry, and see a fine picture every day of his life, in order that worldly cares may not obliterate the sense of the beautiful which God has implanted in the human soul.”
― Johann Wolfgang von Goethe