Sacred Geometry of the Moon

The physical dimensions of Earth and Moon reveal astounding geometries. The sacred geometry of the Moon was understood long ago and the ancients hid the esoteric meaning in the dimensions of their monuments and architecture.

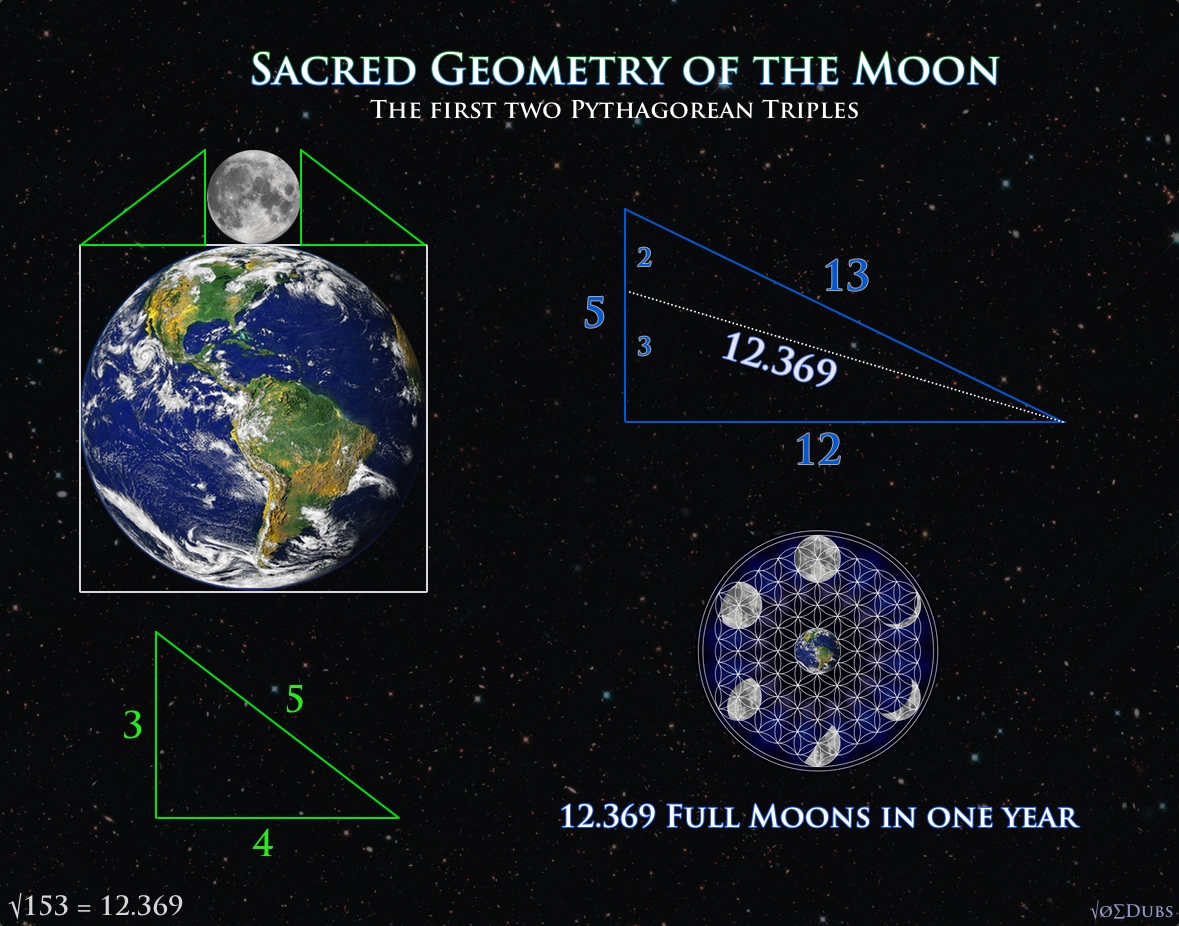
The Moon encodes the first two Pythagorean Triples, which are sets of whole numbers that satisfy the equation popularized by Pythagoras that everyone is familiar with.

Pythagorean Theorem
a^squared + b^squared = c^squared

In the book “Taking Measure”, Scott Onstott shows that the point of intersection that defined the amount of full moons in a year (12.369), lies on the perfect fifth (2:3) ratio on the smallest side of the triangle. These numbers also encode esoteric knowledge about the geometric locations of Stonehenge and other sacred sites in England.

He continues:

“In The Lost Science of Measuring the Earth, John Michell and Robin Heath identified a 5:12:13 Pythagorean triangle that forms a greater temple around Stonehenge that I described in Secrets In Plain Sight – Volume 1. Lundy Island is the right angle point of the triangle, with Stonehenge due East, and due north the quarry in the Preseli hills of Wales where the bluestones used in Stonehenge were mined. There are 12 months in the solar year but 13 resonates with the Moon. Most years have 12 full moons but every second or third year has 13. The Moon’s dance with the Sun is complicated. Calculating the date of Easter, which is tied to both the Moon and the Sun, is a kind of calendrical rocket science. The most harmonious interval in any dance is the musical fifth. If this tone is struck it forms a just 3:2 interval. Michell and Heath drew a line from Stonehenge to the 3:2 point on the line between Lundy and Preseli and discovered that not only does it go to a giant 50 menhir on Caldey Island that a priory church is built around, but its proportion measures 12.369 which is the number of full moons in a year (99.99%). This is also the square root of the number 153 (to 5 significant digits), which has esoteric, religious, and architectural significance, see Key Numbers.”

Taking Measure

pythagorean triples

Pythagoras

The story of the quadrature (squaring) of the lune spans 2500 years of history. It is a problem which was first studied by Greek mathematicians of the 5 th century BCE but was not resolved until the middle of the 20 th century CE when the Russian mathematicians Tschebotaryov and Dorodnov proved what had been suspected for some time, that only five such lunes existed. A lune is the crescent-like figure formed by intersecting two circles. To square a lune is to construct using only straight-edge and compass a square that has the same area. You can’t just measure the area of the lune then construct a square with the same area; you have to construct the square from the lune.

Early Greek mathematicians were fascinated by three classical problems: doubling the cube (called the Delian Problem), trisecting the angle, and squaring the circle; that is constructing a square equal in area to a given circle. They also classified problems by the means used to solve them. According to Pappas of Alexandria (ca. 320 CE) plane problems could be solved in the plane using only straight-edge and compass constructions, solid problems could be solved using conic sections and linear problems required the use of more complicated curves (Heath p. 218; Boyer p. 204). The means used to square the lune discussed here are planar: straight-edge and compass only!

The 5 th century BCE Greek mathematician Hippocrates of Chios (not to be confused with the more famous physician, Hippocrates of Cos) is credited with finding three squarable lunes. According to a 6 th century CE commentary on Artistotle by Philoponus, Hippocrates was originally a merchant who “fell in with a pirate ship and lost all his possessions” (Calinder p. 59) although other sources imply he was a not-so-clever merchant who was defrauded by corrupt tax-officials (van der Waerden p. 131). In any case he went to Athens to pursue his case against those who defrauded him, a process which apparently took a long time and whose outcome is not known. While in Athens he “consorted with philosophers” (Calinder p. 59) and becoming proficient in geometry used his new found talent to become a teacher. He is credited with writing a book on geometry (which was lost), finding a non-planar solution to the Delian problem of doubling the cube (which involved finding the solution to a double mean proportion) and, as already mentioned, squared the lune. In his book, van der Waerden (van der Waerden p. 132) suggests that Hippocrates’ interest in squaring the lune might have stemmed from the similar problem of squaring the circle. Indeed the 3 rd century CE writer Alexander of Aphrodisiensis credits Hippocrates with showing that if a certain kind of lune can be squared, then the circle can be squared  – Brian J. Shelburne

The sum of the 17 Apollo lunar missions equals 153

http://www4.wittenberg.edu/academics/mathcomp/bjsdir/TheFiveLunes120408.pdf

http://www.freemasons-freemasonry.com/occult_philosophy.html

https://en.wikipedia.org/wiki/Lune_(geometry)